倍精度浮動小数点数doubleは53 bitしか精度がありません。
これを超える精度で計算したいけれど多倍長演算は遅いので避けたい、というときに役立つのがdouble-double(疑似四倍精度)です。
double-doubleはその名の通り、doubleを二つ組み合わせることで高い精度を実現します。
double-douleでは数を二つのdoubleの和として表現します。
これにより、double-dobuleは最低*1でも107 bitの精度を実現します*2。
double-double演算ライブラリ
基本
double-doubleの演算は単純ではない(例えば足し算をするとき、ベクトルのように要素ごとに加算すればいいというわけではない)ので、通常はライブラリが用いられます。
C++を利用しているのであれば、kvというヘッダオンリー精度保証付き演算ライブラリに入っているkv::ddを利用するのが最も簡単でしょう。
kv/kv at master · mskashi/kv · GitHub
以下、double-doubleの型をddと書きます。
さて、double-doubleのライブラリを作るときに実装しなければいけない関数は、たくさんあります。
もちろん、dd fma( dd, dd, dd )だけ作ってしまえば、効率はともかく計算することはできます。
それだと無意味な演算が頻発して遅すぎるので、命令数の少ない実装を提供したいということです。
通常の意味で実装が必須となるのは、add関数とmul関数です。
これに加えてfmaも存在すればうれしいですが、kvやcrlibmのライブラリには含まれていませんでした。
十分な精度を持つように実装するのが難しいのでしょうか。
提供されるべきadd関数とmul関数は以下の通りです。
dd add( double, double )……TwoSumと呼ばれるdd演算を実装するときの基本パーツなので提供しないことは実質あり得ないdd mul( double, double )……TwoProdと呼ばれるdd演算を実装するときの基本パーツなので提供しないことは実質あり得ないdd add( double, dd )およびdd add( dd, double )dd mul( double, dd )およびdd mul( dd, double )dd add( dd, dd )dd mul( dd, dd )
TwoSumとFastTwoSum
TwoSumは、二つの倍精度浮動小数点数の和をdouble-doubleで求めるアルゴリズムであり、次の実装が知られています。
dd TwoSum( double a, double b ) {
double x = a + b;
double tmp = x - a;
return { x, a - (x-tmp) + (b-tmp) };
}
しかしこれには6演算も必要でコストが高いです。
実は、a >= bであれば、以下の実装(FastTwoSumとかQuickTwoSumとか呼ばれる方式)で問題ありません。
dd FastTwoSum( double a, double b ) {
double x = a + b;
return { x, a - x + b };
}
TwoProd
TwoProdは二つの倍精度浮動小数点数の積をdouble-doubleで求めるアルゴリズムです。
それを浮動小数点数演算だけで実現できることは、Dekkerが1971年に示しました。
しかしそのアルゴリズムは非常に技巧的なもので、17 FLOPもかかる高コストなものとなっています。
実は、融合積和演算が使えるのであれば、以下の非常に単純なコードで求めることができます。
dd TwoProd( double a, double b ) {
double x = a * b;
return { x, fma( a, b, -x ) };
}
TwoFMAとFastTwoFMA
TwoFMAは倍精度浮動小数点数の融合積和演算の結果をdouble-doubleで求めるアルゴリズムです。
以下のようにできるそうです(参考文献[1])。
dd TwoFMA( double a, double b, double c ) {
double r = fma( a, b, c );
auto[u,du] = TwoProd( a, b );
auto[x,dx] = TwoSum( c, du );
auto[y,dy] = TwoSum( u, x );
double z = y - r + dy;
return { r, z + dx };
}
倍精度浮動小数点数の融合積和演算の結果はdouble-doubleで表せるとは限りませんが、triple-double(double三つの和)でなら表せます。
その場合は、最後のz + dxをFastTwoSum(z, dx)に置き換えれば目的を達成できます。
fma( a, b, c )をdouble-double精度で求めるのに18もの浮動小数点数演算が必要ですが、a*bが-0.5*cとcの間の数となる場合は以下の方法が使えます(たぶん)。
dd FastTwoFMA( double a, double b, double c ) {
double x = fma( a, b, c );
return { x, fma( a, b, c - x ) };
}
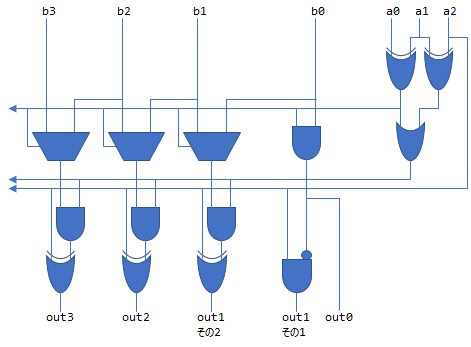
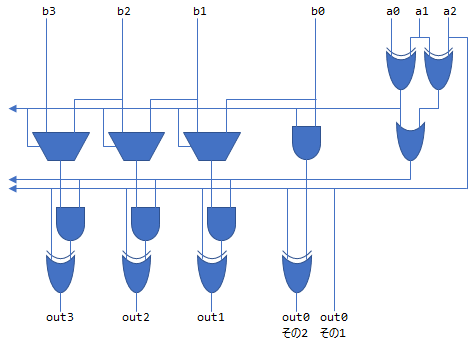
FastTwoFMAからTwoProdとFastTwoSumが導出できる
FastTwoFMAをながめてみると、以下のことがわかります(正確には零の符号とかが怪しいですが、ここでは気にしないでください)。
FastTwoSum( a, b )はFastTwoFMA( b, 1.0, a )と本質的に同じ計算を行っているTwoProd( a, b )はFastTwoFMA( a, b, 0.0 )と本質的に同じ計算を行っている
したがって、原理的にはFastTwoFMAを一度実装してしまえば、適宜1.0や0.0を代入することでFastTwoSumとTwoProdは自動的に導出できそうです。
※TwoFMAは内部でTwoSumとTwoProdを使っていますから、TwoFMAからTwoSumとTwoProdを導くことでTwoSumとTwoProdの実装をサボるというのは無理です。
コンパイラの最適化では自動導出できない
残念ながら、FastTwoFMA( a, b, 0.0 )と書いても、TwoProd( a, b )のように二演算にはならず、余計なごみが残ってしまいます。
これは零にも符号が存在し、(-0.0) + (+0.0)が(-0.0)ではなく(+0.0)になるため、単に+ (+0.0)を無視する、というわけにはいかないためです。
この場合に限ってはFastTwoFMA( a, b, -0.0 )と書くことでclangなら見抜いて二演算にしてくれますが、一般には-0.0を利用することは無理です(a * ±0.0みたいな項も無視してもらいたいですが、この項の符号はaが決まらないとわかりません)。
また、FastTwoFMA( a, 1.0, 0.0 )は{ a, a-a }を返します。
a - aは基本的には恒等的に0.0ですが、aがNaNである場合はそうでないため、それを気にしているようです。
このように、浮動小数点数演算の奇妙な性質が最適化を妨げてしまいます。
コンパイラの最適化に頼るだけでは、FastTwoFMAを実装するだけで効率的なFastTwoSumやTwoProdを手に入れることはできないようです。
コンパイルオプションで対処できる
今回の目的においてコンパイラの最適化を妨げているのは、NaNの存在と零の符号の存在です。
これらはそれぞれ、-fno-honor-nansオプションと-fno-signed-zerosオプションを設定することで問題を解決できます。
-fno-honor-nansだけでは、a - aが0.0になって-0.0ではないので無駄な命令が残ります。
ただし、ライブラリとして提供するからには、利用者にこのような非標準的なコンパイルオプションを強要するのは避けたいところです。
式テンプレートを利用した自動導出
このような問題が発生するのは、具体的な浮動小数点数である1.0や0.0を代入してコンパイラの最適化に任せているからです。
そんなことをしなくても、記号的に演算を変形していけばよいはずです。
C++上で式を記号的に取り扱うためには、式自体をオブジェクトとしてとりあつかう式テンプレートというテクニックを使えばよいです。
以前は中間変数へのコピーをなるべく減らす(大仰な)手段の実装に出現することで知られていましたが、ムーブセマンティクスが登場して以降はそのような目的での使用は下火になった感があります*3。
以下は、式テンプレートを用いてZeroとOneを記号的に取り扱い、それによってdd FastFMA( double, double, double )とdd FastFMA2222( dd, dd, dd )だけからいろいろな関数を導出してみた例です。
本質的にはC++03程度の機能で実装できると思われますが、C++17で追加されたif constexprを使うと記述が非常に読みやすくなります(SFINAEを使ったオーバーロードは優先順位がつけにくいため多くの定義を書く必要があります)。
なお、dd FastFMA2222( dd, dd, dd )の実装は、参考文献[2] 715行目 MulAdd22を参考に、問題なさそうなところ*4をfmaを使って書き換えたものとしています。
#include <cmath>
#include <utility>
static constexpr struct Zero {} zero;
static constexpr struct One {} one ;
template<size_t ID>
struct Var{ double v; double evaluate() const { return v; } };
template<class T, class U>
constexpr bool is_same_impl( T, U ) { return false; }
template<class T>
constexpr bool is_same_impl( T, T ) { return true; }
#define is_same(a,b) is_same_impl( decltype(a){}, decltype(b){} )
template<class T>
struct Neg { T v; double evaluate() const { return -v.evaluate(); } };
template<class A>
auto operator-( A a ) { return Neg<A>{ a }; };
template<class T>
auto operator-( Neg<T> a ) { return a.v; }
auto operator-( Zero ) { return zero; }
template<class A, class B>
struct Add { A a; B b; double evaluate() const { return a.evaluate() + b.evaluate(); } };
template<class A, class B>
auto operator+( A a, B b ) {
if constexpr( is_same( a, -b ) ) {
return zero;
}
else if constexpr( is_same( a, zero ) ) {
return b;
}
else if constexpr( is_same( b, zero ) ) {
return a;
}
else return Add<A, B>{ a, b };
}
template<class A, class B>
constexpr bool is_same_impl( Add<A, B>, Add<B, A> ) { return true; }
template<class A, class B>
auto operator-( A a, B b ) {
if constexpr( is_same( a, zero ) ) {
return Neg<B>{ b };
}
else return a + -b;
}
template<class A, class B, class C>
struct FMA { A a; B b; C c; double evaluate() const {
if constexpr( is_same( c, zero ) ) {
return a.evaluate() * b.evaluate();
}
else return std::fma( a.evaluate(), b.evaluate(), c.evaluate() );
} };
template<class A, class B, class C>
auto fma( A a, B b, C c ) {
if constexpr( is_same( a, zero ) || is_same( b, zero ) ) {
return c;
}
else if constexpr( is_same( a, one ) ) {
return b + c;
}
else if constexpr( is_same( b, one ) ) {
return a + c;
}
else return FMA<A, B, C>{ a, b, c };
}
template<class A, class B, class C>
constexpr bool is_same_impl( FMA<A, B, C>, FMA<B, A, C> ) { return true; }
template<class A, class B>
auto operator*( A a, B b ) { return fma( a, b, zero ); }
#undef is_same
using dd = std::pair<double, double>;
namespace std {
template<> struct tuple_size<Zero> : public integral_constant<std::size_t, 2> {};
template<> struct tuple_size<One> : public integral_constant<std::size_t, 2> {};
template<> struct tuple_element<0, Zero> { using type = Zero; };
template<> struct tuple_element<1, Zero> { using type = Zero; };
template<> struct tuple_element<0, One > { using type = One ; };
template<> struct tuple_element<1, One > { using type = Zero; };
}
template<std::size_t Index> std::tuple_element_t<Index, Zero> get( Zero ) { return {}; }
template<std::size_t Index> std::tuple_element_t<Index, One > get( One ) { return {}; }
template<class T, class U>
dd to_dd( std::pair<T, U> expr ) {
auto [hi, lo] = expr;
return { hi.evaluate(), lo.evaluate() };
}
template<size_t ID1, size_t ID2>
auto Wrap( dd v ) { return std::pair { Var<ID1>{ get<0>( v ) }, Var<ID2>{ get<1>( v ) } }; }
template<class A, class B, class C>
auto FastTwoFMA( A a, B b, C c ) {
const auto hi = fma( a, b, c );
const auto lo = fma( a, b, c - hi );
return std::pair { hi, lo };
}
template<class A, class B>
auto FastTwoSum ( A a, B b ) { return FastTwoFMA( a, one, b ); }
template<class A, class B>
auto TwoProd( A a, B b ) { return FastTwoFMA( a, b, zero ); }
dd AutoFastTwoFMA( double a, double b, double c ) {
return to_dd( FastTwoFMA( Var<0>{ a }, Var<1>{ b }, Var<2>{ c } ) );
}
dd AutoFastTwoSum( double a, double b ) {
return to_dd( FastTwoSum( Var<0>{ a }, Var<1>{ b } ) );
}
dd AutoTwoProd( double a, double b ) {
return to_dd( TwoProd( Var<0>{ a }, Var<1>{ b } ) );
}
template<class A, class B, class C>
auto FastFMA2222( A a, B b, C c ) {
auto [ah, al] = a;
auto [bh, bl] = b;
auto [ch, cl] = c;
auto [t1, t2] = TwoProd( ah, bh );
auto [t3, t4] = FastTwoSum( ch, t1 );
auto t5 = fma( ah, bl, fma( al, bh, cl + t2 + t4 ) );
return FastTwoSum( t3, t5 );
}
dd ddAutoMul( dd a, dd b ) {
return to_dd( FastFMA2222( Wrap<0, 1>( a ), Wrap<2, 3>( b ), zero ) );
}
dd ddAutoFastAdd( dd a, dd b ) {
return to_dd( FastFMA2222( Wrap<2, 3>( b ), one, Wrap<0, 1>( a ) ) );
}
clang++-12.0.1 -std=c++17 -O2 -mfma -cでコンパイルすると、以下の機械語コードが得られます。
0000000000000010 <AutoFastTwoFMA(double, double, double)>:
10: c5 f9 28 d9 vmovapd xmm3,xmm1
14: c4 e2 f9 a9 da vfmadd213sd xmm3,xmm0,xmm2
19: c5 eb 5c d3 vsubsd xmm2,xmm2,xmm3
1d: c4 e2 f9 a9 ca vfmadd213sd xmm1,xmm0,xmm2
22: c5 f9 28 c3 vmovapd xmm0,xmm3
26: c3 ret
0000000000000030 <AutoFastTwoSum(double, double)>:
30: c5 fb 58 d1 vaddsd xmm2,xmm0,xmm1
34: c5 f3 5c ca vsubsd xmm1,xmm1,xmm2
38: c5 f3 58 c8 vaddsd xmm1,xmm1,xmm0
3c: c5 f9 28 c2 vmovapd xmm0,xmm2
40: c3 ret
0000000000000050 <AutoTwoProd(double, double)>:
50: c5 fb 59 d1 vmulsd xmm2,xmm0,xmm1
54: c4 e2 f9 ab ca vfmsub213sd xmm1,xmm0,xmm2
59: c5 f9 28 c2 vmovapd xmm0,xmm2
5d: c3 ret
0000000000000060 <ddAutoMul(std::pair<double, double>, std::pair<double, double>)>:
60: c5 fb 59 e2 vmulsd xmm4,xmm0,xmm2
64: c5 f9 28 ea vmovapd xmm5,xmm2
68: c4 e2 f9 ad ec vfnmadd213sd xmm5,xmm0,xmm4
6d: c4 e2 e9 bd e9 vfnmadd231sd xmm5,xmm2,xmm1
72: c4 e2 f9 bb eb vfmsub231sd xmm5,xmm0,xmm3
77: c5 db 58 c5 vaddsd xmm0,xmm4,xmm5
7b: c5 d3 5c c8 vsubsd xmm1,xmm5,xmm0
7f: c5 db 58 c9 vaddsd xmm1,xmm4,xmm1
83: c3 ret
0000000000000090 <ddAutoFastAdd(std::pair<double, double>, std::pair<double, double>)>:
90: c5 fb 58 e2 vaddsd xmm4,xmm0,xmm2
94: c5 eb 5c d4 vsubsd xmm2,xmm2,xmm4
98: c5 eb 58 c0 vaddsd xmm0,xmm2,xmm0
9c: c5 fb 58 c1 vaddsd xmm0,xmm0,xmm1
a0: c5 fb 58 cb vaddsd xmm1,xmm0,xmm3
a4: c5 db 58 c1 vaddsd xmm0,xmm4,xmm1
a8: c5 f3 5c c8 vsubsd xmm1,xmm1,xmm0
ac: c5 db 58 c9 vaddsd xmm1,xmm4,xmm1
b0: c3 ret
まず、AutoFastTwoFMAとAutoFastTwoSumは三演算、AutoTwoProdは二演算になっているので、この部分は大丈夫そうです。
次に、ddAutoMulですが、非常に小さい値であるa.lo * b.loを無視するタイプのdd乗算の実装が得られています*5。
参考文献[2] 555行目 Mul22と同一なので、これでよさそうです。
最後に、ddAutoFastAddですが、Sloppy*6加算の実装が得られています*7。
参考文献[3] p.5 dd_add・参考文献[4] p.23 Add22・参考文献[5] p.6 SloppyDWPlusDWと同一なので、これで大丈夫そうです。
なお、これらの結果は、このような面倒なことを行わない実装において-fno-honor-nansオプションと-fno-signed-zerosオプションをつけたときと実質的に同じでした。
考察
式テンプレートを使うことで、非標準的なコンパイルオプションに頼らずに、定数伝搬的なことを実現できました。
double-double程度ではライブラリ機能をすべて作るために必要な実装量はそれほど多くないので、それほど役立つようには見えないかもしれません。
しかし、triple-doubleやquad-doubleなどになればadd関数やmul関数の引数の組み合わせは膨大になります。
今回示した方法は、そういう時に役立つかもしれません。
なお、今回はFast系、つまり入力値の大小関係に制限があるものの非分岐な関数を取り扱いました。
一般のadd関数やmul関数はそのような仮定をおけないため、しばしば分岐を含むコードで実装されます。
今回示した方法では、定数伝搬した結果暗黙に成り立つ大小関係を把握することはできません。
しかしそのような場合、実行時にはif文の一方だけが使われることになります。
そのような機械語コードは分岐予測が成功するため、演算ボトルネックであるdouble-double系のプログラムで問題となることは少ないでしょう。
また、今回はFastFMA2222の実装において手動でfmaに変更する最適化を行いました。
しかし、AlderLakeでは浮動小数点数加算が高速であるため、命令数は増えますがfmaを使わずmulとaddに分解したほうがレイテンシを削減できることがあります。
fmaの精度が必要ないところについてはターゲットCPUの特性に応じてfmaにしたりmulとaddにしたり、ということもできたらおもしろそうです。
変数束縛を超えて勝手にfmaにしてはいけないですが、普通の式テンプレートでは変数に束縛されているのか式の途中なのかを区別することができません。
しかし、C++11で追加された右辺値参照を左辺値参照と区別して使うことで、これができるかもしれません。
最後に、今回の手法でも無駄な命令を取り除けないことがあります。
例えば、TwoProdとTwoSumを使わずに加算と乗算だけで実装したTwoFMAを使ってTwoSumやTwoProdを導出することを考えます。
TwoSumの方は導出できるのですが、TwoProdの方は無駄命令だらけになってしまいます。
これは、[d, du] = TwoProd( a, b )のようになっている時、d + du == dなのですが、これを使った定数伝搬ができないことが原因です。
これを自動で実現するのは相当困難なように思えます。
ただ、そういったコードは正規化にこだわる実装には出てきますがSloppyな実装にはあまり出てこないので、Fast系を導出する場合はあまり問題にならないのかもしれません。
まとめ
doubleで精度が足りない時、double-dobleを使うと手軽で便利- double-doubleのライブラリを作るのは面倒(※普通は自分で作らず、kv/kv at master · mskashi/kv · GitHubなどを使うとよいでしょう)
- 式テンプレートを使うことで、double-double用の
fma関数を作るだけで効率の良いaddとmulを自動導出できた
- triple-doubleなどのライブラリを作るときにも役立つと期待
参考文献
- [1] Boldo, Sylvie and Muller, Jean-Michel, "Exact and Approximated Error of the FMA", IEEE Transactions on Computers 60 157–164 (2011).
- [2] David Defour, Catherine Daramy, Florent de Dinechin, Matthieu Gallet, Nicolas Gast, Christoph Lauter, Jean-Michel Muller, "cr-libm, a portable, efficient, correctly rounded mathematical library" (2010).
- [3] 柏木 雅英「double-double 演算、double-double 区間演算に関するまとめ」(2021). http://verifiedby.me/kv/dd/dd.pdf
crlibm/crlibm_private.h at master · taschini/crlibm · GitHub
- [4] Catherine Daramy-Loirat, David Defour, Florent de Dinechin, Matthieu Gallet, Nicolas Gast, Christoph Quirin Lauter, Jean-Michel Muller, "CR-LIBM A library of correctly rounded elementary functions in double-precision" (2006). https://ens-lyon.hal.science/ensl-01529804/file/crlibm.pdf
- [5] Mioara Maria Joldes, Jean-Michel Muller, Valentina Popescu, "Tight and rigorous error bounds for basic building blocks of double-word arithmetic", ACM Transactions on Mathematical Software 44(2), 1–27 (2017). https://hal.science/hal-01351529v3/document