$N$ ビット符号なし乗算器は、 $N$ ビットの符号なし整数二つを受け取り、 $2N$ ビットの符号なし整数を出力する回路です。

$N$ ビット乗算器は、部分積を作る $N^2$ 個のANDゲートと $N(N-2)$ 個の全加算器（full adder, FA）を組み合わせて作ることができます。この構成で全加算器が $N(N-2)$ 個必要なのは、以下のような説明ができます。全加算器は3入力2出力なので信号線を一本減らす効果があります。部分積は全部で $N^2$ 個あり、これを $2N$ 本に減らす必要があります。よって、 $N^2 - 2N = N(N-2)$ 本減らすためには、 $N(N-2)$ 個の全加算器が必要です。

以下では、さらに効率的に乗算器を作るいくつかのテクニックを書き、その後11ビット乗算器を設計してみます。

テクニック

Wallace Tree

Wallace Tree（ワラス木、またはより原音に近くウォレス木）は、 $N(N-2)$ 個の全加算器をどのように配置するかの方法の一つです。 Wallace Treeでは、全加算器をバランスした木状に配置します。順次加算していく方式ではレイテンシが $\Theta(N)$ 段となってしまいますが、バランスした木とすることでレイテンシを $\Theta(\log N)$ 段に抑えます。

実際には、本当に全加算器だけで作ってしまうと桁上げ伝搬加算器（ripple-carry adder）になってしまって、 $\Omega(N)$ 段のレイテンシが不可避です。そこで、各位の信号線の本数が2本になるまではWallace Treeで減らしていって、その先は桁上げ先読み加算器などの高速加算器を使う、といった方法が使われます。 Wallace Treeで各位の信号線が2本になるまで減らすレイテンシが $\Theta(\log N)$ 段、高速加算器のレイテンシが $\Theta(\log N)$ 段、ということで全体として $\Theta(\log N)$ 段のレイテンシが達成できます。

Wallace Treeの模式図として、図1のようなものが紹介されることがあります。しかし、これは「わかっている」技術者向けに書かれた、信号線の減り具合を示すための模式図です。桁上げは次の位に送らなければいけませんから、実際の回路は図2のようになります*1。

図2: 六段のWallace Treeの実際。橙色で示した線は下位からの桁上げ信号

Booth encoding

Booth encoding（ブース符号化）は、部分積を減らす方法の一つです。 Radix-2、Radix-4、Radix-8、……などがあります。

Radix-2 Booth encoding

Radix-2 Booth encodingは、乗数の二進表現に1が連続した部分がある場合、それが（シフトと）足し算一回と引き算一回で実現できるという事実を利用します。普通の乗算器で31倍を実現するには16倍、8倍、4倍、2倍、1倍、の5つの数を足しこむ必要があります。しかし、被乗数の32倍を足し、被乗数の1倍を引く、とすれば実現できます。 Radix-2 Booth encodingは、このような最適化を行うことです。なぜRadix-2 Booth「encoding」というかというと、この手順は乗数を二進表現（各位が0か1）から冗長二進表現（各位が-1か0か1）に変換していることに相当するからです。

31倍のような特殊な数だけではなく、乗数が0b0011111011110のような1が連続している部分がありさえすれば、この手法を適用することで加算の回数を減らすことができます。残念ながら、Radix-2 Booth encodingを用いても加算の回数を減らせない乗数がある（例えば0b010101010101とか）ので、ハードウェア実装には向きません。ハードウェア実装では、最悪に備えて回路を用意しないといけないからです。手回し式計算器を使ったり、乗算器のないCPUで計算したりする際などには役立つようです。あるいは、可変レイテンシの直列乗算器を作るためにも使えそうです。

Radix-4 Booth encoding

Radix-4 Booth encodingはこの仕組みを昇華させたものであり、非常に効率的であるためハードウェア乗算器の実装でよく用いられるようです。この方法では、乗数を二桁ごとに区切って、四進表現（各位が0か1か2か3）から冗長四進表現（各位が-2か-1か0か1か2）に変換します。ここで、各位としてあり得る数に3がなくなっているのが重要です。 3倍は加算器を使わないと表現できませんが、-2倍、-1倍、0倍、1倍、2倍は加算器なしにシフトだけで簡単に作ることができます（※本当は符号反転に加算器が必要ですが解決する方法があります。後述します）。これにより、部分積が乗数の二桁ごとに一つとなるため、加算すべき部分積を半分に減らすことができます。代わりに-2倍・-1倍・0倍・1倍・2倍から選択する回路が必要になりますが、部分積の数が半分になることはWallace Tree約二段分（二段で9本を4本にすることができる）に相当するので、メリットが上回ります。

エンコーディングするためには、a[3:1], a[5:3], a[7:5], a[9:7], ...のように、二桁ずつずれていく重なりのある三桁を取り出す必要があります。具体的には、a×bを計算するとき、

a[2k+1:2k-1]が000なら、bの0倍を出力する
a[2k+1:2k-1]が001か010なら、bの $1\times2^{2k}$ 倍を出力する
a[2k+1:2k-1]が011なら、bの $2\times2^{2k}$ 倍を出力する
a[2k+1:2k-1]が100なら、bの $-2\times2^{2k}$ 倍を出力する
a[2k+1:2k-1]が101か110なら、bの $-1\times2^{2k}$ 倍を出力する
a[2k+1:2k-1]が111なら、bの0倍を出力する

とします。

これに加えてa[0]由来の部分積を作る必要があります。このためには、a[-1]=0だと思ってa[1:(-1)]について同様のエンコーディングを行えばよいです。この項は-2倍か-1倍か0倍か1倍が出てきます。

また、最上位付近をどこまで足さないといけないかも注意が必要です。と言ってもほぼ明らかで、最上位ビットa[N-1]の影響があるところまで足せばよいです。

$N$ が奇数であれば、a[N]=0だと思ってa[N, N-2]の分まで足せばよいです。この項は、0倍か1倍か2倍が出てきます。つまり、負の数は出てきません。

$N$ が偶数であれば、a[N+1]=a[N]=0だと思ってa[N+1, N-1]の分まで足せばよいです。この項は、0倍か1倍が出てきます。つまり普通のANDゲートで作られる部分積です。

Radix-8 Booth encoding

Radix-8 Booth encodingはさらにこの仕組みを発展させたもので、乗数を三桁ごとに区切って八進表現（各位が0, 1, 2, 3, 4, 5, 6, 7のいずれか）から冗長八進表現（各位が-4, -3, -2, -1, 0, 1, 2, 3, 4のいずれか）に変換します。冗長八進表現だとシフトだけでは作れない3倍が必要ですが、これは一回作ってしまえば使いまわせるので、十分大きなビット幅の乗算器であれば加算すべき部分積を三分の一に減らせる効果が上回ります。部分積を三分の一に減らせる効果がRadix-4で部分積を二分の一に減らしたのよりも上回る境界は、3倍を作るコストを考慮に入れても一応 $N=6$ 程度なのでほとんどの乗算器に適用可能に見えます。しかし、3倍を計算するレイテンシは隠蔽できず、またRadix-4とRadix-8の差分は部分積の数が三分の二になること、つまりWallace Tree一段分の効果しかないのでレイテンシを短くする効果はありません。極力トランジスタ数を減らしたいということではない限り、Radix-4で十分に思えます。

符号反転の方法

Booth encodingを行うと、符号なし乗算器を作っているのに負の数が出てきて面倒ですが、うまく取り扱う方法が知られています。以下Radix-4を前提とした説明を行いますが、負の数を取り扱うアイデア自体はRadixによらず適用可能です。

さて、「-2倍、-1倍、0倍、1倍、2倍は加算器なしにシフトだけで簡単に作ることができる」と書きましたが、実際にはこれは正しくありません。符号を反転させるためには、一の補数を取った後に1を足さないといけなくて、ここに加算器が必要だからです。この問題は、最後に足す1を一種の部分積だとみなすことにより解決できます。

また、このままだと符号拡張のためのビットが部分積として残ってしまい、部分積が四分の三に減るにとどまります。ここで、符号拡張で生じる部分積は、すべて0（例えば、0b000000）かすべて1（例えば、0b111111）である点に注目します。あらかじめ0b111111という定数を足す回路を用意しておけば、すべて1の時はそのままでよく、すべて0の時はそれに1を足せばよいです（ $\overline{S}$ を足せばよいです）。また、足す定数は $N/2$ 個（合計 $N^2/4$ ビットくらい）出現しますが、事前にその和を計算しておけば、部分積として入力しなければいけない定数は一つ（ $N$ ビットくらい）にできます。この定数は、Radix-4の時0b010101...0101011になります。なお、この符号拡張をキャンセルする手法は、符号付き乗算器を設計するときにも役立ちます。

さて、この定数の最後は0b011となっていますが、この部分は符号ビットの残り（ $\overline{S_0}$ ）と足し合わせると0b $\overline{S_0}S_0S_0$ になります。このようにすることで、部分積が多い位ができてしまうことを回避できます。

これを説明したのが図3です。最後のRadix-4 Booth乗算器は、図解としてよく見るものと一致しています。

図3: Booth encodingで現れる負の数への対処方法。一つ目：-bを~b+1と表現し、足すべき1も部分積とみなす。二つ目：符号拡張で出現するビットを定数＋符号ビットの反転（ $\overline{S}$ ）のように表現する。三つ目： $\overline{S_0}$ と定数の加算を実行することで、部分積の数は変わらないが位あたりの最大部分積数を削減できる。

図3: Booth encodingで現れる負の数への対処方法。一つ目：-bを~b+1と表現し、足すべき1も部分積とみなす。二つ目：符号拡張で出現するビットを定数＋符号ビットの反転（ $\overline{S}$ ）のように表現する。三つ目： $\overline{S_0}$ と定数の加算を実行することで、部分積の数は変わらないが位あたりの最大部分積数を削減できる。

その他の高速乗算アルゴリズムの適用

相当大きな乗算器でない限り、Karatsuba法やToom–Cook乗算、フーリエ変換を使った乗算などは役に立ちません。計算量がナイーブ法を下回るビット幅が最も小さいKaratsuba法を例にとって、なぜ役に立たないのかを説明します。

Karatsuba法は、乗算回数を減らす代わりに加減算の回数が増える方法です。ここで、ハードウェア乗算器においては、1ビット×1ビットの乗算はANDゲート1つでできる一方、これで生じた信号線を1本減らすには5～6ゲートからなる全加算器が必要です。つまり、ANDゲートより5倍以上大きな全加算器の数が重要であり、その観点からすると乗算と加算はほぼ同じコストです。これがKaratsuba法がビット数が相当大きくない限り役に立たない直観的な理由です。部分積が減って全加算器が減る量と前処理・後処理で全加算器が増えてしまう量の大小により、Karatsuba法を使用すべきかが決まります。

必要な全加算器の数を概算してみます。 Radix-4 Booth乗算器では、全加算器が $\frac1 2 N^2$ 個程度必要です。ここに（再帰的にではなく一段階だけ*2）Karatsuba法を適用すると、前処理に $2N$ 個程度、後処理に $6N$ 個程度の全加算器が必要で、代わりに乗算部分の全加算器を $\frac3 8 N^2$ 個程度に減らせます。これが釣り合うのは $N=64$ の時です。したがって、Radix-4 Booth encodingを使用していれば、64ビット乗算器まででKaratsuba法を使うメリットは全くありません。同様の計算により、128ビット乗算器であってもRadix-16 Booth encodingを採用すれば十分で、Karatsuba法を採用するメリットはなさそうだということがわかります。それ以上、例えば256ビット乗算器を作る際には、Karatsuba法が役立つかもしれません。

Toom-2.5はさらに加算が多いので、相当大きなビット数でないとメリットがありません。 Radix-16 Booth encodingを前提にすると、1024ビット乗算器あたりでKaratsuba法に追いつくようです。 Toom-3以降は係数に $\frac1 6$ などが出てきてもう一度乗算（循環小数定数での乗算なので実質的には $\Theta(\log N)$ 回の $N$ ビット加算）が必要なので、実用するのはほぼ不可能でしょう。フーリエ変換などなおさらです。

Wallace Treeの実際の設計

基本

Wallace Treeを設計するには、図4のように各位に何本の信号線があるかを書いたExcelシートを使うと便利です。この時、各位にある信号線を3（全加算器の入力数）で割って切り捨てた数だけ、その位に全加算器を配置します。これを何段か繰り返して、すべての位で信号線の本数が2以下になったとき、Wallace Treeが終了します（図5）。

アンチパターン

ただし、これだけだと各位の信号線の本数が上位ビットから「2, 2, 2, ..., 2, 2, 3」などとなった時、桁上げ伝搬加算器ができてしまいます。この時にのみ、半加算器（half adder, HA）を使います。半加算器は、2入力2出力で信号線の本数が減らないので極力使いたくないですが、アンチパターンが発生した場合だけは使うことでWallace Treeの段数を大幅に削減することができます。その設計を行ったのが図6です。

図7のようにもっと前の段から半加算器を使うことで段数を削減できることがあるようですが（Dadda乗算器と関係している？）、よくわかっていません。

11ビット符号なし乗算器の設計

なぜ11ビットを選んだかというと、半精度浮動小数点数（IEEE754のbinary16）の仮数部が（暗黙の1を含めて）11ビットだからです。基本的には、Wallace TreeとRadix-4 Booth encodingを組み合わせて設計します。定数との加算を実行し、0b $\overline{S_0}S_0S_0$ とするタイプで設計します。

すると、図8のようになります。

0b $\overline{S_0}S_0S_0$ を使うタイプで設計したため、一つの位あたりの最大の信号線の本数は六本となり、うまく三段に収めることができました。

Radix-4 Booth乗算器を素直に作ると、各位に所属する部分積の個数の分布がきれいな山形にならずギザギザした感じになるので、半加算器を多く使う必要があるようです。この問題を解決するため、Booth encoderを工夫し、先に一桁だけ桁上げを行ってしまうことを考えます。すると、図9のようになります。

各位に所属する部分積の個数の分布がきれいな山形になったためか、半加算器の数を7から4に減らすことができました。

さて、「先に一桁だけ桁上げを行う」という部分で回路が増えていたら半加算器の数が減っても意味がありません。そこで、その部分の回路を実際に確認してみます。先に一桁だけ桁上げを行うRadix-4 Booth encoderの-2倍/-1倍/0倍/1倍/2倍、を選択する回路は以下を出力すればよいです。

a[2:0]	出力	...	out[3]	out[2]	out[1]その2	out[1]その1	out[0]
000	0b	...	0	0	0	0	0
001	1b	...	b[3]	b[2]	b[1]	0	b[0]
010	1b	...	b[3]	b[2]	b[1]	0	b[0]
011	2b	...	b[2]	b[1]	b[0]	0	0
100	-2b	...	~b[2]	~b[1]	~b[0]	1	0
101	-1b	...	~b[3]	~b[2]	~b[1]	~b[0]	b[0]
110	-1b	...	~b[3]	~b[2]	~b[1]	~b[0]	b[0]
111	0b	...	1	1	1	1	0

この回路は、図10のように実現することができます。

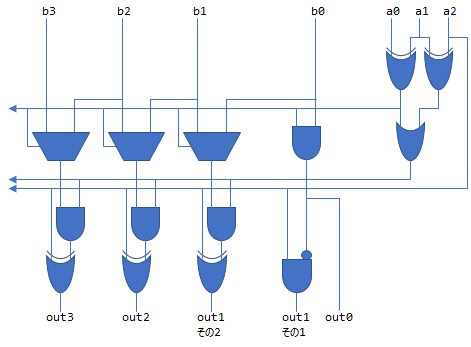
これに対して通常のRadix-4 Booth encoderは図11のような回路となります。

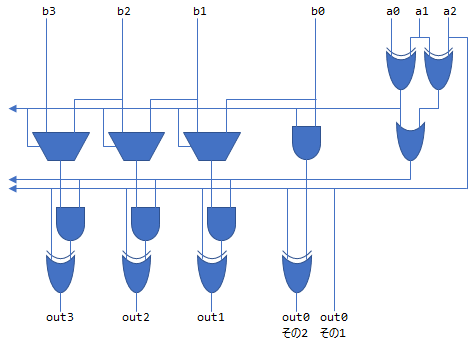
ほぼ回路は変わっていないため、先に一桁だけ桁上げを行うことで半加算器を減らすメリットを受けられることがわかりました。

Verilog HDL実装

ここまでの実装をVerilog HDLで記述しました。この実装は、あり得る2²²通りの入力すべてに対して正しい答えを返すことをVerilatorにより確認しています。

module multiplier11(lhs, rhs, result);
    input  wire[10:0] lhs;
    input  wire[10:0] rhs;
    output wire[21:0] result;

    function[11:0] Radix_4_Booth_select_012;
        input [1:0] a;
        input[10:0] b;

        case( a )
        2'b000: Radix_4_Booth_select_012 = 12'b0;
        2'b001: Radix_4_Booth_select_012 = { 1'b0, b };
        2'b010: Radix_4_Booth_select_012 = { 1'b0, b };
        2'b011: Radix_4_Booth_select_012 = { b, 1'b0 };
        endcase
    endfunction

    function[14:0] Radix_4_Booth;
        input [2:0] a;
        input[10:0] b;
        Radix_4_Booth[14] =  1'b1;
        Radix_4_Booth[13] = ~a[2];
        Radix_4_Booth[12:1] = Radix_4_Booth_select_012( a[1:0] ^ {2{a[2]}}, b );
        if(a[2])
            Radix_4_Booth[12:2] = ~Radix_4_Booth[12:2];
        Radix_4_Booth[0] = a[2] & ~Radix_4_Booth[1];
    endfunction

    function[15:0] Radix_4_Booth_lsb;
        input [1:0] a;
        input[10:0] b;
        Radix_4_Booth_lsb[15] = ~a[1];
        Radix_4_Booth_lsb[14] =  a[1];
        Radix_4_Booth_lsb[13] =  a[1];
        Radix_4_Booth_lsb[12:1] = Radix_4_Booth_select_012( a[1:0] ^ { 1'b0, a[1] }, b );
        if(a[1])
            Radix_4_Booth_lsb[12:2] = ~Radix_4_Booth_lsb[12:2];
        Radix_4_Booth_lsb[0] = a[1] & ~Radix_4_Booth_lsb[1];
    endfunction

    function[11:0] Radix_4_Booth_odd_msb;
        input [1:0] a;
        input[10:0] b;
        Radix_4_Booth_odd_msb = Radix_4_Booth_select_012( a, b );
    endfunction

    wire[15:0] a0b  = Radix_4_Booth_lsb    (lhs[ 1:0], rhs);
    wire[14:0] a2b  = Radix_4_Booth        (lhs[ 3:1], rhs);
    wire[14:0] a4b  = Radix_4_Booth        (lhs[ 5:3], rhs);
    wire[14:0] a6b  = Radix_4_Booth        (lhs[ 7:5], rhs);
    wire[14:0] a8b  = Radix_4_Booth        (lhs[ 9:7], rhs);
    wire[11:0] a10b = Radix_4_Booth_odd_msb(lhs[10:9], rhs);

/*
    assign result =   { 7'b0, a0b[15:1]        } + { 20'b0, a0b[0], 1'b0 }
                    + { 6'b0, a2b[14:1],  2'b0 } + { 18'b0, a2b[0], 3'b0 }
                    + { 4'b0, a4b[14:1],  4'b0 } + { 16'b0, a4b[0], 5'b0 }
                    + { 2'b0, a6b[14:1],  6'b0 } + { 14'b0, a6b[0], 7'b0 }
                    + {       a8b[14:1],  8'b0 } + { 12'b0, a8b[0], 9'b0 }
                    + {      a10b      , 10'b0 } ;
*/

    function[1:0] full_adder;
        input a;
        input b;
        input c;
        full_adder = { a&b|b&c|c&a, a^b^c };
    endfunction

    wire[1:0] x3  = full_adder(a0b[ 4], a2b[ 2], a2b[ 0]);
    wire[1:0] x4  = full_adder(a0b[ 5], a2b[ 3], a4b[ 1]);
    wire[1:0] x5  = full_adder(a0b[ 6], a2b[ 4], a4b[ 2]);
    wire[1:0] x6  = full_adder(a0b[ 7], a2b[ 5], a4b[ 3]);
    wire[1:0] x7  = full_adder(a0b[ 8], a2b[ 6], a4b[ 4]);
    wire[1:0] x8  = full_adder(a0b[ 9], a2b[ 7], a4b[ 5]);
    wire[1:0] x9  = full_adder(a0b[10], a2b[ 8], a4b[ 6]);
    wire[1:0] x10 = full_adder(a0b[11], a2b[ 9], a4b[ 7]);
    wire[1:0] x11 = full_adder(a0b[12], a2b[10], a4b[ 8]);
    wire[1:0] x12 = full_adder(a0b[13], a2b[11], a4b[ 9]);
    wire[1:0] x13 = full_adder(a0b[14], a2b[12], a4b[10]);
    wire[1:0] x14 = full_adder(a0b[15], a2b[13], a4b[11]);
    wire[1:0] y9  = full_adder(a6b[ 4], a8b[ 2], a8b[ 0]);
    wire[1:0] y10 = full_adder(a6b[ 5], a8b[ 3], a10b[0]);
    wire[1:0] y11 = full_adder(a6b[ 6], a8b[ 4], a10b[1]);
    wire[1:0] y12 = full_adder(a6b[ 7], a8b[ 5], a10b[2]);
    wire[1:0] y13 = full_adder(a6b[ 8], a8b[ 6], a10b[3]);
    wire[1:0] y14 = full_adder(a6b[ 9], a8b[ 7], a10b[4]);
    wire[1:0] y15 = full_adder(a6b[10], a8b[ 8], a10b[5]);
    wire[1:0] y16 = full_adder(a6b[11], a8b[ 9], a10b[6]);
    wire[1:0] y17 = full_adder(a6b[12], a8b[10], a10b[7]);
    wire[1:0] y18 = full_adder(a6b[13], a8b[11], a10b[8]);
    wire[1:0] y19 = full_adder(a6b[14], a8b[12], a10b[9]);

    wire[1:0] z5  = full_adder( x5 [0], x4 [1], a4b[0]);
    wire[1:0] z6  = full_adder( x6 [0], x5 [1], a6b[1]);
    wire[1:0] z7  = full_adder( x7 [0], x6 [1], a6b[2]);
    wire[1:0] z8  = full_adder( x8 [0], x7 [1], a6b[3]);
    wire[1:0] z9  = full_adder( x9 [0], x8 [1], y9 [0]);
    wire[1:0] z10 = full_adder( x10[0], x9 [1], y10[0]);
    wire[1:0] z11 = full_adder( x11[0], x10[1], y11[0]);
    wire[1:0] z12 = full_adder( x12[0], x11[1], y12[0]);
    wire[1:0] z13 = full_adder( x13[0], x12[1], y13[0]);
    wire[1:0] z14 = full_adder( x14[0], x13[1], y14[0]);
    wire[1:0] h15 = full_adder(a2b[14], x14[1],  1'b0 ); // Half Adder
    wire[1:0] z15 = full_adder(a4b[12], y14[1], y15[0]);
    wire[1:0] z16 = full_adder(a4b[13], y15[1], y16[0]);
    wire[1:0] z17 = full_adder(a4b[14], y16[1], y17[0]);
    wire[1:0] z20 = full_adder(a8b[13], a10b[10], y19[1]);

    wire[1:0] w7  = full_adder(z7 [0], z6 [1], a6b[0]);
    wire[1:0] w8  = full_adder(z8 [0], z7 [1], a8b[1]);
    wire[1:0] w9  = full_adder(z9 [0], z8 [1],  1'b0 ); // Half Adder
    wire[1:0] w10 = full_adder(z10[0], z9 [1], y9 [1]);
    wire[1:0] w11 = full_adder(z11[0], z10[1], y10[1]);
    wire[1:0] w12 = full_adder(z12[0], z11[1], y11[1]);
    wire[1:0] w13 = full_adder(z13[0], z12[1], y12[1]);
    wire[1:0] w14 = full_adder(z14[0], z13[1], y13[1]);
    wire[1:0] w15 = full_adder(z15[0], z14[1], h15[0]);
    wire[1:0] w16 = full_adder(z16[0], z15[1], h15[1]);
    wire[1:0] w17 = full_adder(z17[0], z16[1],  1'b0 ); // Half Adder
    wire[1:0] w18 = full_adder(y18[0], z17[1], y17[1]);
    wire[1:0] w19 = full_adder(y19[0],  1'b0 , y18[1]); // Half Adder
    wire[1:0] w21 = full_adder(a8b[14], a10b[11], z20[1]);

    assign result =  { w21[0], w19, w17, w15, w13, w11, w9, w7, z5, x3, a0b[3:1] }
                   + { 1'b0, z20[0], w18, w16, w14, w12, w10, w8, 1'b0, z6[0], 1'b0, x4[0], 1'b0, a2b[1], a0b[0], 1'b0 };
endmodule

full_adderの入力としてどれを選ぶかは改善の余地があります。今回は信号の名前がなるべくレギュラーになるように配置しましたが、実際は桁上げ信号の配線が短くなるように選ぶとよいでしょう。また、複合ゲートが使える場合はa&b|b&c|c&aより~(a&b|b&c|c&a)の方が少ないトランジスタ数で作れるので、一部の全加算器は負論理としたほうが良いかもしれません。

符号ビットキャンセル定数伝搬最適化

符号ビットキャンセル定数となんらかの部分積を入力として持つ半加算器は定数伝搬によりほぼノーコスト（NOTゲート一つ）となります。これを三か所に適用することで、三つの半加算器をなくせるようです。

小さな高速加算器を使う

単純に考えると最終段の高速加算器の幅は22ビットとなりますが、下位をWallace Tree実行中に桁上げ伝搬加算器で求めれば高速加算器の幅を縮めることができます。下位のどこまでを確定させられるかを考えてみると、

2⁰の位は部分積が1つなので既に確定している
2¹の位はWallace Treeの一段目で確定できる
2²の位はWallace Treeの二段目で確定できる
2³の位はWallace Treeの三段目で確定できる

となります。また、最上位ビットは高速加算器のキャリー出力（これは高速加算器の結果が出る一段前に出力される）とのXORで作れるので、ここも高速加算器を通す必要がありません。

ここまでの結果から、高速加算器は2⁴の位から2²⁰の位までを取り扱えばよいことがわかりました。高速加算器の幅が17ビットとなり、微妙に二冪を超えているのでいまいちです。試行錯誤してみたところ、1bit+2bit加算器と半加算器を適切な位置に配置すれば、2⁴の位もWallace Treeの三段目で確定できることがわかりました。 1bit+2bit加算器は、図13に示すような4ゲートからなる3入力3出力の回路*3で、全加算器よりも小さいのでこれを使うことは問題ないはずです。 out[1]出力の遅延が全加算器一段分よりやや長い気もしますが、ここはクリティカルパスではないので問題ありません。

これにより高速加算器の幅を16ビットとした設計が図14です。

まとめ

乗算器を作るために有用な二つのテクニック
- Wallace Tree
- (Radix-4) Booth encoding
実際に11ビット符号なし乗算器を設計した
- 先に一桁だけ桁上げするRadix-4 Booth encoderを使うことで半加算器を減らせる
- 符号ビットキャンセル定数を伝搬させることで半加算器を減らせる
- 1bit+2bit加算器を導入することで、高速加算器の幅を16ビットにすることができた