Leading Zero Count (LZC) は、二進法で表された符号なし整数の上位に0が何個連続しているかを数えることです。例えば、32ビット符号なし整数で考えると、LZC(0x80000000)は0、LZC(0x7fffffff)は1、LZC(5)は29、LZC(2)は30、LZC(1)は31、LZC(0)は32、などです。

これに対し、Leading Zero Anticipation (LZA) は、二進法で表された符号つき整数A, Bを受け取り、A+Bを直に計算することなしにLZC(A+B+1)を（多少の誤差の範囲で）予測することです*1。 A+Bの計算なんて非常に軽量（普通のCPUなら1 cycleで可能）なのだから省略する意味はないのでは、と思うかもしれません。しかし、 $N$ ビットの加算器のハードウェアは $\Theta(\log N)$ 段のゲートからなるのが普通*2なので、意外とレイテンシが長いです。 A+Bの計算を省略したいのはこのためであり、つまりハードウェアを作る場合にのみ利用価値のあるアルゴリズムだということです。

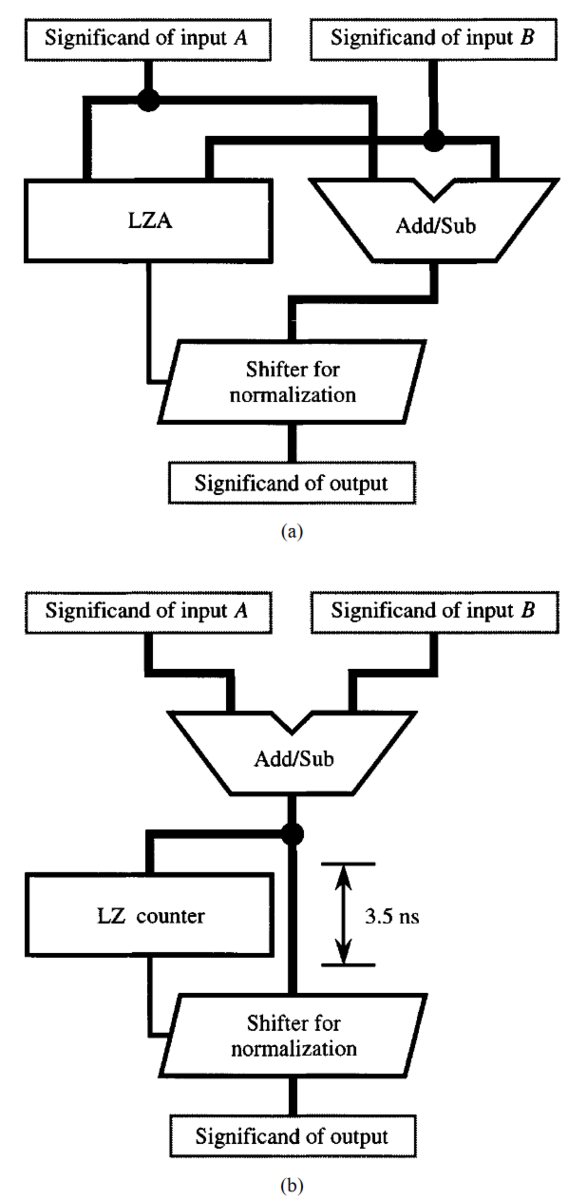
実際にどのような場合に役立つのかを見てみると、低レイテンシの浮動小数点数加算器を作るときに使われるようです。普通に浮動小数点数加算器を作ろうと思うと、1. 入力を桁合わせする、2. それらを加算器に入力する、3. その結果のLZCを求める、4. 加算結果をLZC分だけシフトする、5. 丸める、という手順で仮数部を算出します。ここで、「2. 加算器に入力する」→「3. その結果のLZCを求める」という部分が直列になっています。 LZAを使えば、加算の計算と並列してLZAの計算ができるので、その分だけ4. の手順に早くたどり着くことができます。図1は、これを表した図です。

図1: (a)LZAを用いた場合 (b)LZCを用いた場合（参考文献[1]より引用）

以下、参考文献[1]で紹介されているアルゴリズムを紹介します。このLZAアルゴリズムは、LZC(A+B+1)またはLZC(A+B+1)-1を予測します。

アルゴリズム

仮定

LZAの計算では、A+B+1の計算でオーバーフローが起きないことを仮定します。浮動小数点数加算器を作ることにLZAを利用する場合、これを仮定することは妥当です。

AとBが同符号（足し算）の場合：繰り上がりすることを見越してAやBよりも1ビット広い加算器を使うはずなので、オーバーフローは発生しない。
AとBが異符号（引き算）の場合：適宜左右オペランドを交換するはずなので、LZAの入力は $A\ge-B$ と仮定でき、オーバーフローは発生しない。

なお、LZAの出力は、使う加算器のビット幅を $N$ ビットとして、 $\log N$ ビットの整数（0～N-1）です。A+B+1は0になることがないため、LZCと違い $N$ を出力することがありません。

概略

LZAのアルゴリズムは、以下の手順によります。

まず、A+B+1の近似値Eを計算する。
次に、LZA(A, B)をLZC(E)で求める。

非常にシンプルでわかりやすいアルゴリズムです。もちろん、重要なのは、どのようにEを計算するかです。 Eの具体的な計算手順は後で示しますが、重要なのはEが以下の条件を満たすように計算されることです。

A+B+1 ≦ E ≦ 2A+2B+1

この時、LZA(A, B) ≦ LZC(A+B+1) ≦ LZA(A, B)+1となります。なぜなら、以下が成り立つからです。

A+B+1 ≦ Eなので、LZC(A+B+1) ≧ LZC(E) = LZA(A, B)が成り立つ。
E ≦ 2A+2B+1なので、LZC(A+B+1) = LZC(2A+2B+1)+1であることに注意して、LZC(A+B+1) = LZC(2A+2B+1)+1 ≦ LZC(E)+1 = LZA(A, B)+1が成り立つ。

Eの計算

具体的なEの計算方法の説明をします。重要なのは、 $O(1)$ 段の回路で計算しないと意味がないということです。

足し算の場合

足し算の場合、Eの計算は適当で大丈夫です。例えば、E = (i|j)<<1|1とかで十分です。ほかにもいろいろ解があります。

実際には、引き算の時と回路を共有したいです。引き算の時用の回路の方が複雑になるので、まずは引き算の時用の回路を作ってみて、それが足し算の時でも正しく動くかを確認することにしましょう。

引き算の場合

変数Xの2ⁱの位を $X_i$ と表すことにします。 $E_i$ は、 $A_i, B_i, A_{i-1}, B_{i-1}$ のみを用いて、ビット毎に計算します。作戦としては、

A+B+1の計算結果で、上位の0が連続するビットには、1を立てない
A+B+1の計算結果で、最も上位の1が立つビットかその一つ左に、1を立てる
下位は適当でよい（0でも1でもよい）ので、上の二条件を満たす簡単な回路を流用する

という感じです。

さて、どのようにA+Bを計算しないままに、A+B+1の計算結果が0になるところを見分けるのかということになります。ここで、Aと-Bが打ち消しあって（浮動小数点数演算の用語でいうところの桁落ちが発生して）上位に0に並ぶパターンは、以下の二つしかないことに注目します（ $A\ge-B$ が満たされていることに注意します）。

Aの上位が100000...となっていて、-Bの上位が011111...となっている
- AとBは上位が100000...となり、XOR(A,B)は上位に0がならぶ
Aと-Bの上位ビットが完全に同じ
- XOR(A,B)は上位に1がならぶ

そこで、次のようにすれば、「A+B+1の計算結果で、上位の0が連続するビットには、1を立てない」を満たせそうです。

$A_i$ と $B_i$ が同じで、 $A_{i-1}$ と $B_{i-1}$ がどちらも0なら、 $E_i$ は0
$A_i$ と $B_i$ が違うなら、 $E_i$ は0

「 A+B+1の計算結果で、最も上位の1が立つビットかその一つ左に、1を立てる」を満たすには、次のようにすればよいです。

$A_i$ と $B_i$ が同じで、 $A_{i-1}$ と $B_{i-1}$ のどちらかが1であれば、 $E_i$ は1

本当にこれでよいのでしょうか。別の視点から考えてみます。

Aのiビット目以上とBのiビット目以上を足すと0になるとします。ここで、Aの $2^{i-1}$ の位かBの $2^{i-1}$ の位のどちらかが1であるパターンを考えます。この時、 $2^{i-1} \lt A+B+1 \lt 2^{i+1}$ となるので、Eの $2^i$ の位を1にすればよいです。なぜなら「 $2^i$ の位に繰り上がりが発生して、A+B+1の最上位の1は $2^i$ の位（LZCはLZAに等しい）」「 $2^i$ の位に繰り上がりが発生せず、A+B+1の最上位の1は $2^{i-1}$ の位（LZCはLZAより1大きい）」のどちらかが発生し、いずれの場合でも出力の要求を満たすからです。もう一方のパターン、つまりAの $2^{i-1}$ の位とBの $2^{i-1}$ の位のどちらもが0である場合は、Aのi-1ビット目以上とBのi-1ビット目以上を足しても0になるので、iを一つ減らして同じことを考えればよいです。

よって、

$E_i = \lnot (A_i \oplus B_i) \land (A_{i-1} \lor B_{i-1})$

とすればよいです。先と同じ結論が得られました。なお $E_0$ は範囲外アクセスですが、1としておけば要求を満たせます（ $E_0$ はLZAが $N$ になってしまうのを防ぐためにしか使われません）。

足し算の場合の確認

Eは、Aの最上位ビットかBの最上位ビットのどちらか上にあるほうの一つ上の位に1が立つので、これで大丈夫です。

C言語 ソースコード

#include <stdio.h>
#include <assert.h>

unsigned lza(unsigned A, unsigned B) {
        unsigned E = ~(A^B) & (A|B)<<1 | 1;
        assert( A+B+1 <= E && E <= A+A+B+B+1 );

        // calculate LZC(E) without addition
        unsigned Q2  = (E  & 0xaaaaaaaa) | (E <<1 & 0xaaaaaaaa) | (~E  & 0xaaaaaaaa)>>(2-1);
        unsigned Q4  = (Q2 & 0x88888888) | (Q2<<2 & 0x88888888) | (~Q2 & 0x88888888)>>(4-2)
     | (((Q2 & 0x88888888)>> 3)*1 & Q2>>2 | ((~Q2 & 0x88888888)>> 3)*1 & Q2) & 0x11111111;
        unsigned Q8  = (Q4 & 0x80808080) | (Q4<<4 & 0x80808080) | (~Q4 & 0x80808080)>>(8-3)
     | (((Q4 & 0x80808080)>> 7)*3 & Q4>>4 | ((~Q4 & 0x80808080)>> 7)*3 & Q4) & 0x03030303;
        unsigned Q16 = (Q8 & 0x80008000) | (Q8<<8 & 0x80008000) | (~Q8 & 0x80008000)>>(16-4)
     | (((Q8 & 0x80008000)>>15)*7 & Q8>>8 | ((~Q8 & 0x80008000)>>15)*7 & Q8) & 0x00070007;
        return Q16 & 15;
}

unsigned lzc(unsigned x) {
        if( x & 1<<15 ) { return  0; }
        if( x & 1<<14 ) { return  1; }
        if( x & 1<<13 ) { return  2; }
        if( x & 1<<12 ) { return  3; }
        if( x & 1<<11 ) { return  4; }
        if( x & 1<<10 ) { return  5; }
        if( x & 1<< 9 ) { return  6; }
        if( x & 1<< 8 ) { return  7; }
        if( x & 1<< 7 ) { return  8; }
        if( x & 1<< 6 ) { return  9; }
        if( x & 1<< 5 ) { return 10; }
        if( x & 1<< 4 ) { return 11; }
        if( x & 1<< 3 ) { return 12; }
        if( x & 1<< 2 ) { return 13; }
        if( x & 1<< 1 ) { return 14; }
        if( x & 1<< 0 ) { return 15; }
        return 16;
}

int main() {
        // Add
        for( unsigned i = 0; i < (1<<15); ++i ) {
                for( unsigned j = 0; j < (1<<15); ++j ) {
                        assert( lzc(i+j+1) == lza(i,j) || lzc(i+j+1) == lza(i,j)+1 );
                }
        }
        // Sub
        for( unsigned i = 0; i < (1<<15); ++i ) {
                for( unsigned j = 0; j <= i; ++j ) {
                        assert( lzc(i+~j+1) == lza(i,~j) || lzc(i+~j+1) == lza(i,~j)+1 );
                }
        }
}

参考文献

[1] Hiroaki Suzuki, Hiroyuki Morinaka, Hiroshi Makino, Yasunobu Nakase, Koichiro Mashiko, Tadashi Sumi, "Leading-Zero Anticipatory Logic for High-Speed Floating Point Addition", IEEE Journal of Solid-State Circuits 31(8), 1996.

*1:「+1」部分を不思議に思うかもしれませんが、LZC(X-Y)を予測するためにLZA(X, ~Y)のように入力したいからです。コーナーケースであるLZC(0)を回避する意味合いもあるかもしれません。

*2:最上位ビットの計算は入力のすべてのビットの影響を受けるため、入力数が定数個以内のゲートを使う限り、明らかにo(log N)段は無理です。また、プリフィックス加算器と呼ばれる構成を使えば、O(log N)段は達成できます。

よーる

Leading Zero Anticipation (LZA) の勉強